Physics and Code - Harmonic Oscillators

Nero - Jun 28 2023

Wait hold on, what we doing? Why you doing a blog post bout physics?

Okay, first, let me fill you in with some context: I was on the verge of failing Physics AP 1. It’s got the standard electric field, electromagnetic field, optics, and one of the coolest things in my opinion: waves.
Now, I hated waves and haven’t given any thought to understanding them, but waves are everywhere around us. Every communication that is “wireless” is through waves. Sound is just waves that are actually being intercepted by our ears, everything we see is because of light which is a wave that collides with objects and is being intercepted by our eyes, internet is waves, as well.
Needless to say, all around us there's waves.

All I’ve told you until now is actually true (at least to my knowledge, I might be wrong, I'm still not that good at physics), but this isn’t what is cool for me. What’s cool for me is what the graph of a harmonic damped oscillator looks like and how we’d translate it into actual animations in our browser.
Let me show you a graph of the harmonic damped oscillator's movement:

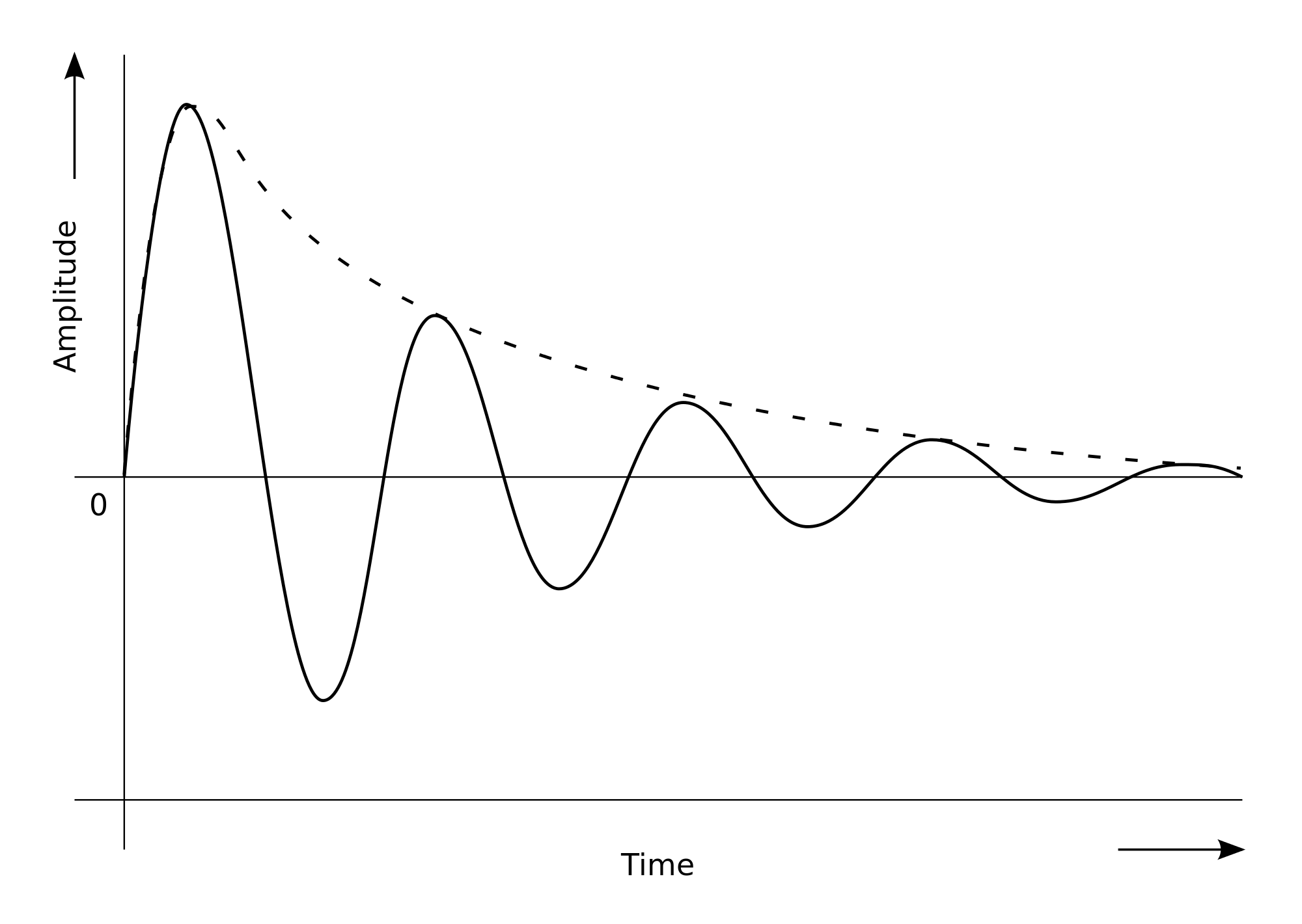You see what I mean? The wave type thing that's like getting smaller and smaller (the Amplitude goes to 0).
I think that's pretty cool and I'd like to make that into an animation of some sort either with the canvas or CSS with some text, color/light in the background and some masking thingy.

Also, here's a video where you can see the actual movement in real life

How does the damped oscillator work?

I know you didn't ask for this, but let's take a moment to actually understand the physics behind the actual damped oscillator (also, you can see the damped oscillatory motion here: YOUTUBE

Aight, so the plan is:

We go through Newton's laws
We go through the normal (undamped) oscillator
We understand the damped one
Newton's laws Newton's got 3 laws of motion that are used to describe the relationship between the motion of an object and the forces acting on it which are the next 3:
1. A body remains at rest, or in motion at a constant speed in a straight line, unless acted upon by a force.
2. When a body is acted upon by a force, the time rate of change of its momentum equals the force.
3. If two bodies exert forces on each other, these forces have the same magnitude but opposite directions.

Now, for this specific experiment we're gonna use the first 2 laws.
Let's recap the first two to be more easily understood.

The first one is inertia, basically, let's think of a car as a body. And as for our environment we'll consider a perfect environment without any kind of friction. Now let's say the car got to a certain speed, let's say 60mph (100kmh), and it maintains this speed constant. Now if we were to just let the car on the highway, to with that speed, it won't stop at all, it would continue on the highway, in a straight line.
Now, after some time on the highway, that highway leads to a city and in that city, there's buildings. High chances that the car will collide with one of the buildings and be stopped. As there would be a force applied by that building that would stop it instantly (kind of related to 3rd law, but we ain't getting into that for this one).

The second law is basically the $F = m * a$ formula but rewritten, as follows: $a = F / m$ . Basically, if in our environment/system that we had before there was some kind of friction (friction with the road, the air) and we were to not burn any fuel to maintain our speed of 60mph, we would slow down, as the friction would lower our momentum.

The undamped oscillator

The undamped oscillator, which is also called harmonic oscillator, is just that, an oscillator, it oscillates.
Let's say we got a ball attached to a string which in turn is attached to a wall.
Now, if we were to let the ball sit so that the string wouldn't be stretched nor compressed, we would call this the equilibrium position. Because the restoring force ( $F = -kx$ ) wouldn't actually come into effect.
The $F = -kx$ force is the restoring force which tries to restore the string to be in its equilibrium position.

Let's remind ourselves of our experiment when talking about Newton's motion laws. We were talking about a perfect system, one in which we wouldn't have any friction (there wouldn't be any loss of energy to the surroundings, but we tryna keep it simple for now). If we have no friction what will actually happen is the next thing:
We have some initial displacement (we either stretch or compress the string). Let's say we stretch the string and after we let go, the restoring force will try to restore the string to its equilibrium position. Since there is no friction, it will not stop, so the restoring force will get the displacement, at some point in time, to be 0, which would mean that we are in the equilibrium position, but it will also go and compress itself to the same absolute value of displacement that we had before, but with the opposite sign.
So if before we had the displacement equal to -3cm now we'd have it +3cm. Graphing it out would look something like this:

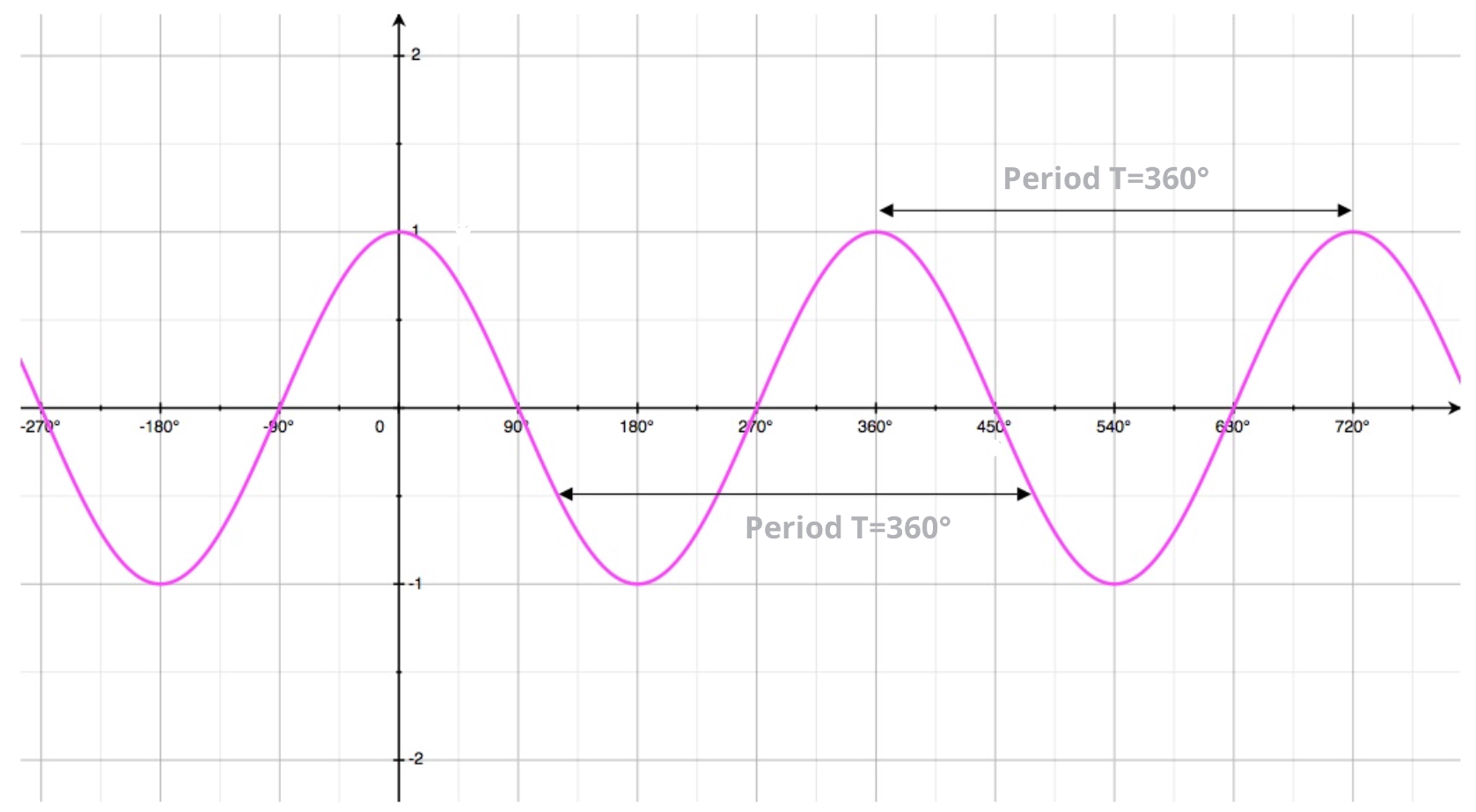
Where the amplitude would be 3cm.

Now, as we know, each graph comes from some kind of mathematical formula, and the motion for the harmonic oscillator is not that different:

$x(t) = x_0 + A * cos(ωt + φ)$

Let's see what each of these mean:

Well, first, let's look at the left side of the equation, we got $x(t)$ . $x$ is basically a function that depends on $t$ . So, basically, the displacement depends on the the time spent since $t_0$ , which is usually $0$ .

Going to the right side of the equation we have:

$x_0$ , which is the equilibrium position, which we also take as $0$ as we choose the origin of our coordinate system such that $x_0$ is $0$ . Nothing crazy here, we just take it as it is.
$A$ , which is the amplitude, which is basically the maximum absolute value of the displacement
$cos(ωt + φ)$ $cos (ω t + φ)$ , which is where the fun lies. Now the cosine is a trigonometric function, and in this context it is basically used for showing the oscillation, it doesn't have a specific name in our context, and we'll explain it in a little more detail in a bit, but for now, let's see what the argument of it is composed of:
- $ω$ , which is called angular frequency, it kind of shows how many cycles per second happen (it's not exactly that, as $ω = 2π/T$ , and $T$ is basically the period, which is defined as the time it takes for the object to complete one oscillation (cycle) and return to its initial position) - long story short, is some kind of frequency, and frequency is how many times something happens per second
- $t$ , which is basically how many seconds have passed since $t_0$ , it's basically time
- φ, which is called phase constant, I honestly don't know how to easily explain this to you, but I'll try my best: it's basically, let's say we don't use $t_0$ to say the Amplitude is maximum, but a little less, but not 0

Here's a link that'll explain more labman.phys.utk.edu

Okay, so we kind of went over what the general equation is. Let's dumb it down to something easier to grasp and good for our use case:

$x(t) = A * cos(ωt)$

Good, this is much easier, right?

Now let's dive into the cosine trigonometric function, what in the duck is going on and why are we using it?

Well, the cool thing about both sine and cosine is that they are kind of oscillating, take a look at cosine's graph:

It's literally our undamped harmonic oscillator.
It's just how it is, ion know what to tell you if you got more questions about it.

Well, I kind of do, for one more specific question... Why do we use cosine instead of sine?

Well, the cool thing about cosine in this specific situation is that... $cos(0) = 1$

So basically, at $t = 0$ , so our starting point, when we stretched the string to the maximum, we can say that $x(0) = A * cos(ω * 0)$ which is basically $x(0) = A$ , so we are fully stretched at $t = 0$ , which is our starting position. This is pretty crazy you got to admit.

And then, cosine starts to go down to 0, and then -1, and then goes back up to 0, and 1, and we are at our starting position after a full cycle, or period.

So yeah, this is the undamped harmonic oscillator, it's basically oscillations.

The damped harmonic oscillator

To be quite honest with you, everything that was crazy we went over when explaining the undamped harmonic oscillator. Which is the base for the damped one.

Now, for the damped harmonic oscillator, all that we need to do is... just add some friction. Now, let's think of it, when we add some friction what happens is... with each cycle that passes by, the amplitude goes down, because friction makes it so we get closer and closer to the equilibrium position with the displacement (basically displacement goes to 0) every cycle.

So, all we have to do is make the amplitude a function of time:

$x(t) = A * \exp(-βt) * cos(ωt + φ)$

Aaaaaand, when I told you that we went over everything that was crazy, I lied. Not really, we are not gonna get into how specifically the damped oscillator formula looks like and explain it fully because:

$x(t) = C_1e^{-δ+\sqrt{δ^2-ω_0^2}t} + C_2e^{(-δ-\sqrt{δ^2-ω_0^2})t}$

If y'all think I'm gonna go over this, y'all tweakin.

How do we code this?

Thank you for asking, we're gonna make use of our javascript buddy to help us with all sorts of animations. You're gonna love this (I have no clue how are we going to code this, but I like the idea, and we gonna do it).

For prototyping we'll use p5.js, as we can create animations and such.

Now, before actually hopping in, let me tell you EXACTLY what I want to do. Animate a ball so that it traverses the graphed function.
If you remember, our function is basically a unidimensional function, we got $x$ (the displacement) as a function depending on $t$ , the time.

Now graphing it out, that line is bi-dimensional, we got an x and y for every point of the line.

The x-axis represents the time and y-axis represents the displacement at any given point in time.

Let's see how this will look in p5.js:

function setup() {
  // First we create the canvas with a 800px width and 800px height
  createCanvas(800, 800);
  
  // We set the framerate to 60fps
  frameRate(60);
}

var positions = [];

function draw() {
  // Honestly, idk what this exactly does besides giving the background a gray-ish look
  background(220);

  // Now, we calculate the x and y coordinates based on time
  // The easiest way to do that is using the frame count, let me explain:
  // The framecount starts at 0 and is directly proportional with the time, so we can just figure out the time by dividing it to how many frames there are in a second (/ 60)
  
  
  // Our x (which is the position on the x-axis, not the displacement) is going to be the framecount times a constant (that we can change) modulo the width (so that when it goes off the right side of the screen we can just reset it)
  var x = (frameCount * 1.15) % width;
  
  // Our y is the actual x (the displacement)
  // var y = x_0        + A   * cos(omega * t)
     var y = height / 2 + 100 * cos(frameCount * 0.07);
  
  // ChatGPT stuff so that it draws last positions of the ball
  positions.push(createVector(x, y));
  if(positions.length > 400){
    positions.shift();
  }
  noFill();
  stroke(200);
  for (var i = 0; i < positions.length; i++) {
    var pos = positions[i];
    ellipse(pos.x, pos.y, 10, 10);
  }
  // ChatGPT stuff so that it draws last positions of the ball

  // Now we just draw the point, this is literally ChatGPT I'm not even gonna hide it, was too lazy to read the docs on all these
  stroke(0);
  strokeWeight(20);
  point(x, y);
}

If anybody actually wants to play with it, here is the sketch

Now, to make it follow the graph of a damped harmonic oscillator, we only need to add the exp function call (which is basically just Euler's number raised to the argument provided)

function setup() {
  createCanvas(800, 800);
  frameRate(60);
}

var positions = [];

function draw() {
  background(220);

  var x = (frameCount * 1.15) % width;
  
  // here, we added the exponential, which lowers the amplitude over time, and it's a function of x so that when it restarts and goes to the left of the screen it gets the same amount of amplitude that it had when starting out (or close to)
  // var y = x_0        + A   * cos(omega * t)         * exp(- beta * t)
     var y = height / 2 + 100 * cos(frameCount * 0.07) * exp(- 0.1  * x/60);
   
  positions.push(createVector(x, y));
  if(positions.length > 400){
    positions.shift();
  }
  noFill();
  stroke(200);
  for (var i = 0; i < positions.length; i++) {
    var pos = positions[i];
    ellipse(pos.x, pos.y, 10, 10);
  }
  
  stroke(0);
  strokeWeight(20);
  point(x, y);
}

If anybody wants to play with it, here is the sketch

Now, let's see if we can actually use the formula of the damped oscillator for something. What I was thinking was to manipulate the saturation of the color of a text using the formula so in the end the intensity would be the lowest possible.
I might have lost some of you, and that's fine, so let me fill you in real quick.

When we talking about a color, we are talking about 3 main things:

Hue
Value
Saturation

What we are interested in right now is the saturation. It essentially is the intensity of a color. As the saturation increases, the color appears more pure, more like the actual color. As the saturation decreases, the color appears more washed-out or pale. learn.leighcotnoir.com
Cool thing about the HSL (Hue, Saturation, Lightness) format is that the web supports it so we can easily play with it.

For example, red is: hsl(0, 100%, 50%). Turn down the saturation to 0 (hsl(0, 0%, 50%)) and all of a sudden we got gray!

Coding it real quick leads us to:

<!DOCTYPE html>
<html>
<head>
</head>
<body>
  <h1 style="color:hsl(0, 0%, 50%)">Crazy Ahh Text</h1>
  <script>
    const angularFrequency = 0.1;
    const ampltitude = 1;
    const dampingCoefficient = 0.001;
    const callDelay = 100;
    const expResultThreshold = 0.003;

    /**
     * @param {number} saturationPercentage
     * @description This is the function that basically changes the saturation
     * */

    function setSaturation(saturationPercentage) {
      /** @type {HTMLHeadingElement} */
      const h1 = document.getElementById("crazyAhhText");
      h1.style.color = `hsl(0, ${saturationPercentage}%, 50%)`;
    }

    // calls is going to be the variable that is tied to the time
    // this is because we increment calls every time the setInterval's handler is called
    // which atm happens every __callDelay__ milliseconds
    let calls = 0;

    const interval = setInterval(() => {
      // we calculate the Math.exp result, with time this becomes really small
      // And when it does, we can conclude that the time spent has increased quite a bit
      // So that we can clear the setInterval and not modify the color of the text anymore
      const expResult = Math.exp(-1 * dampingCoefficient * calls);

      // Set the saturation to 0 and clear the interval so we don't change the text anymore
      if(expResult < expResultThreshold){
        setSaturation(0);
        clearInterval(interval);
        return;
      }

      // It's basically this formula but changed a bit to actually fit our current environment
      // x(t) = A * exp(-beta*t) * cos(omega * t);

      const result = (ampltitude *
        expResult *
        Math.cos(angularFrequency * calls) ) * 100 % 100
  
      setSaturation(
        result.toFixed(2)
      )

      // Increment calls so we can actually see change!
      calls++;
    }, callDelay);
  </script>
</body>
</html>

To see it in action go to codepen.io

And yeah, I don't know, ain't nothing that fancy, but still something that might be used at some point in time by someone.

Till next time!