ANTIBOTS - PART VIII - Geetest - CFF
In-Depth Control-Flow-Flattening Analysis
Introduction
Today we are taking a look at what Control Flow Flattening really means. We will go through different examples (from easy to hard), explain my process of thought, maybe even talk about some edge-cases, and finally we will work on a real example: A part of a Geetest script related to its captcha. The Geetest script can be found at gcaptcha4.js - while also being available on this blog's repo.
Also, this article is somewhat of a rewrite of my last article on antibots, part VII, where I was taking a look at incapsula. Check that out, as well, if you want. (though, not needed).
What is CFF (Control Flow Flattening)
As the name suggests, CFF aims to flatten the flow of a program. It is an obfuscation technique used in many obfuscators nowadays, be it in interpreted languages (such as javascript) but also in compiled ones (C/C++ - for more info visit obfuscator.re). We take the time to mention obfuscator.io and jscrambler as the 2 main javascript obfuscators that are known to me and use this technique. The former can be tested for free, while for the latter I am not sure how permissive is the trial.
Mini example:
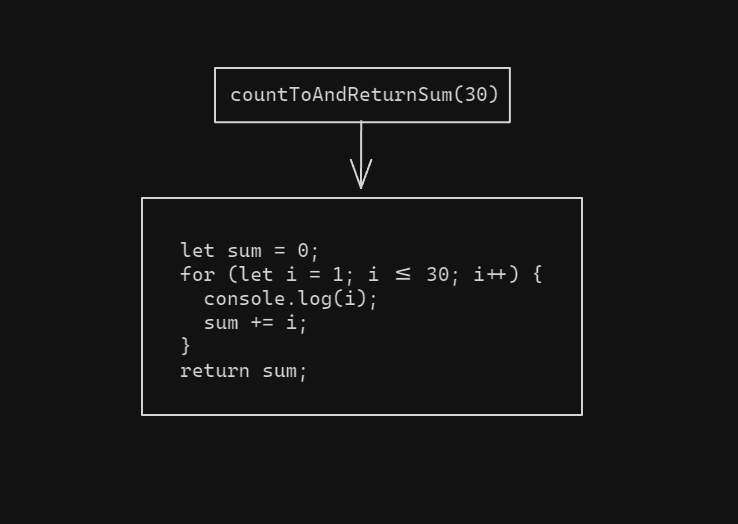
In the next 2 code blocks we have a function that does the same thing: takes a number, console logs every number from 1 to our given number and then returns the sum of all the numbers it went through. It looks something like this:
function countToAndReturnSum(num) {
let sum = 0;
for (let i = 1; i <= 30; i++) {
console.log(i);
sum += i;
}
return sum;
}
countToAndReturnSum(30);
A Control-Flow Flattened program would look something like this:
function countToAndReturnSum(num) {
let jmp_var = 2;
while (jmp_var != 42) {
switch (jmp_var) {
case 7:
console.log(i);
sum += i;
i++;
jmp_var = 4;
break;
case 2:
var sum = 0;
var i = 1;
jmp_var = 4;
break;
case 9:
return sum;
break;
case 4:
jmp_var = i <= num ? 7 : 9;
break;
}
}
}
countToAndReturnSum(30);
As you can see our beautiful and well-understood function has had its flow modified. If we were to graphically show it, back when it was clean, it would look like this:
Now, the obfuscated version looks more like this:
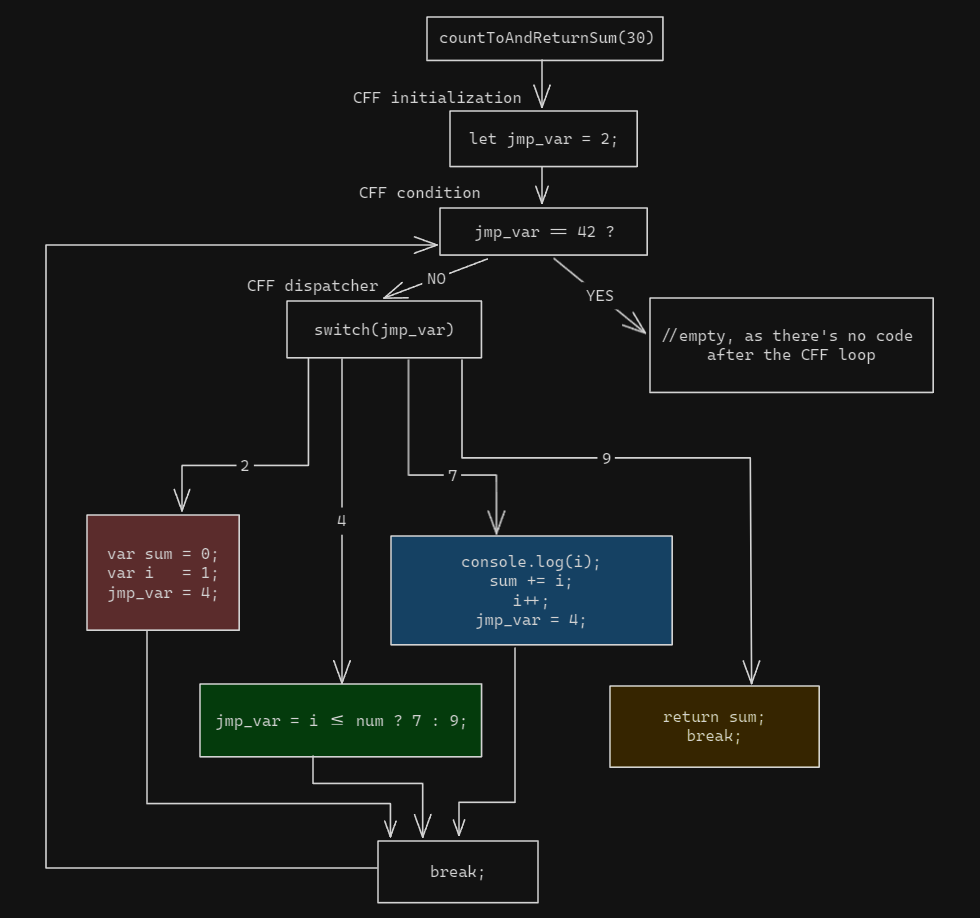
The first version is pretty straightforward and if you have a bit of programming experience you should be able to read it without any problems. The second one is a tad more complicated. The steps of the program have been broken down in pieces (the switch statement's cases) and then placed in a random order (at least in the code, in the diagram they are in order LTR). This is not the easiest example, nor the hardest, but it exists to give you an idea if you are not that familiar with CFF.
We'll get back to this example a bit later, for now let's see some easier ones and explain my process of thought.
Examples
1. Easy
From
function add(a + b){
let sum = a + b;
return sum;
}
To
function add() {
let jmp_var = 2;
for (; jmp_var !== 42; ) {
switch (jmp_var) {
case 2:
var sum;
sum = a + b;
jmp_var = 7;
break;
case 7:
return sum;
break;
}
}
}
First, let's note a change. Instead of a WhileStatement we have a ForStatement. Taking into account the specific Loop type (WhileStatement / ForStatement / DoWhileStatement) is not an edge case (or could be, if we are talking about JSCrambler, as I've seen only ForStatements used by them).
Second, this is one of, if not, the easiest example there is. Our code has been split in 2 cases inside the switch case.
Now, what is our problem, what are we trying to do? Well, we are trying to deflatten our flattened code. How do we this? For this example (and possible for all, until the last one) we'll do it manually:
- we keep track in our mind that the starting value for the
jmp_varis 2 - we check the condition of the
ForStatementto make sure we can even get in it and execute (let's say the condition would bejmp_var === 42thus making the code inside theForStatementto never execute) - we go inside the
ForStatementand theSwitchStatementand focus on theSwitchCasethat has thetestproperty's value aNumericLiteralnode having the value2 - we copy, in a file, the
Statements inside theSwitchCase's body, excluding theBreakStatementand theAssignmentExpressionwhere we assign a value to thejmp_varvariable - we keep in mind the new value and restart the process, going back to step 2, but this time the value will be
7
In the end, your file should contain the next code:
function add(a, b) {
// here is where you place the collected Statements
var sum;
sum = a + b;
return sum;
}
And there we have it, our first deflattened example. It only gets harder and worse from here.
But, before going to the 2nd example, let us dissect it a little bit and see how we could (or better said) should think of this problem in terms of computers. After all, we want the computer to run it all.
Well, we can think of this switch cases as nodes of a graph, better said, an oriented graph. Why is that? Every node points to another node, as we've seen (Edge case! Some nodes might not point to any other, our 2nd case (case 7) has only a return statement, no AssignmentExpression to change the jmp_var). Knowing the starting node (its value, the jmp_var variable value), we could traverse the graph, collect the needed statements and recreate the initial program (more or less).
Rewriting our flattened add function as a graph, we'd have:
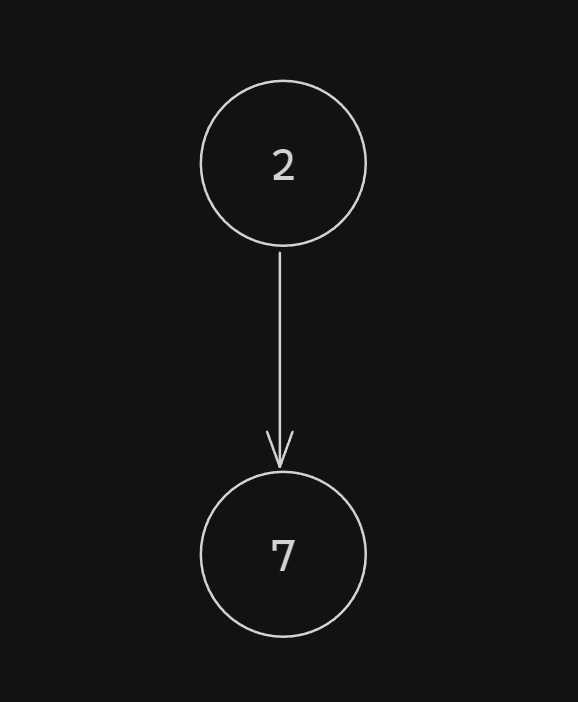
Simply, the first node (2) links to the second node (7).
(P.S. This is called a CFG - Control Flow Graph)
2. Medium
From
function countToAndReturnSum(num) {
let sum = 0;
console.time(`countToAndReturnSum(${num})`);
for (let i = 1; i <= num; i++) {
console.log(i);
sum += i;
}
console.timeEnd(`countToAndReturnSum(${num})`);
return sum;
}
countToAndReturnSum(30);
To
function countToAndReturnSum(num) {
let jmp_var = 2;
while (jmp_var != 42) {
switch (jmp_var) {
case 7:
console.log(i);
sum += i;
i++;
jmp_var = 4;
break;
case 2:
var sum = 0;
var i = 1;
jmp_var = 5;
break;
case 5:
console.time(`countToAndReturnSum(${num})`);
jmp_var = 4;
break;
case 9:
console.timeEnd(`countToAndReturnSum(${num})`);
return sum;
break;
case 4:
jmp_var = i <= num ? 7 : 9;
break;
}
}
}
countToAndReturnSum(30);
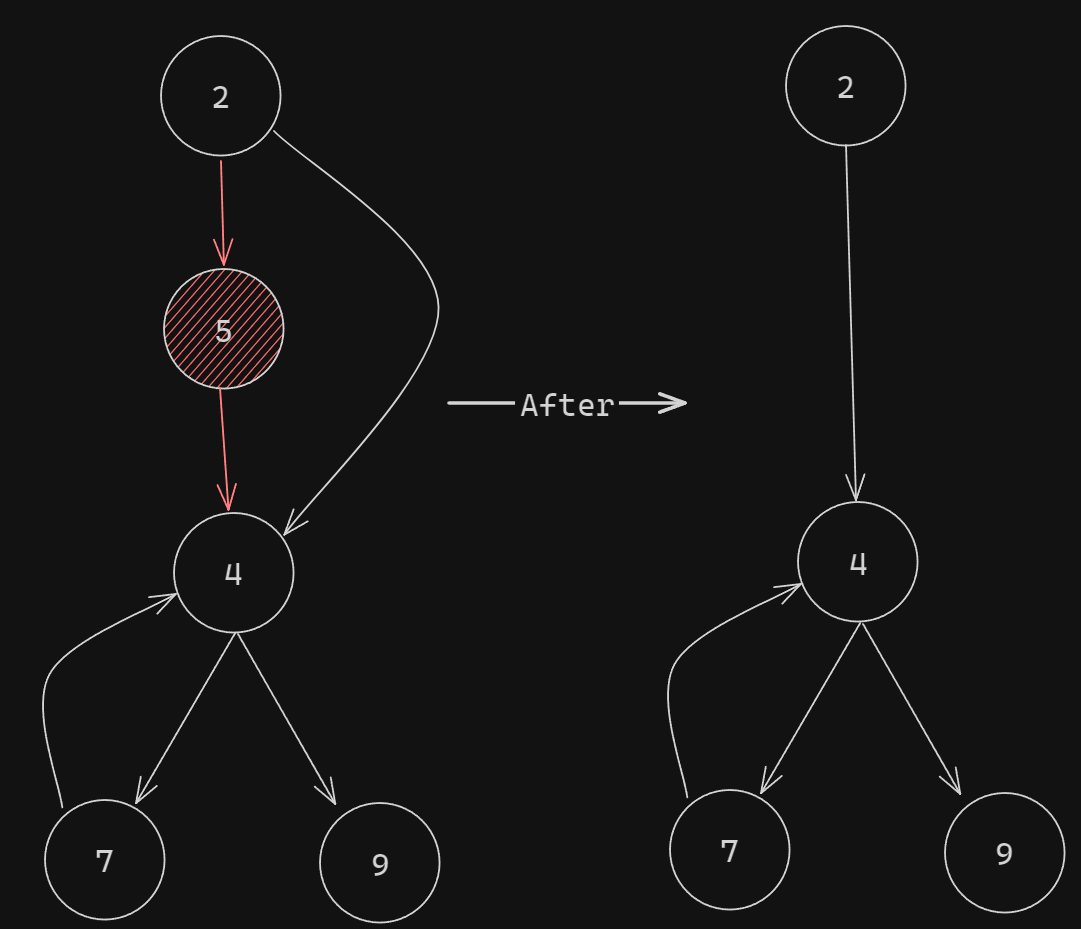
Let me redo the diagram for this one:
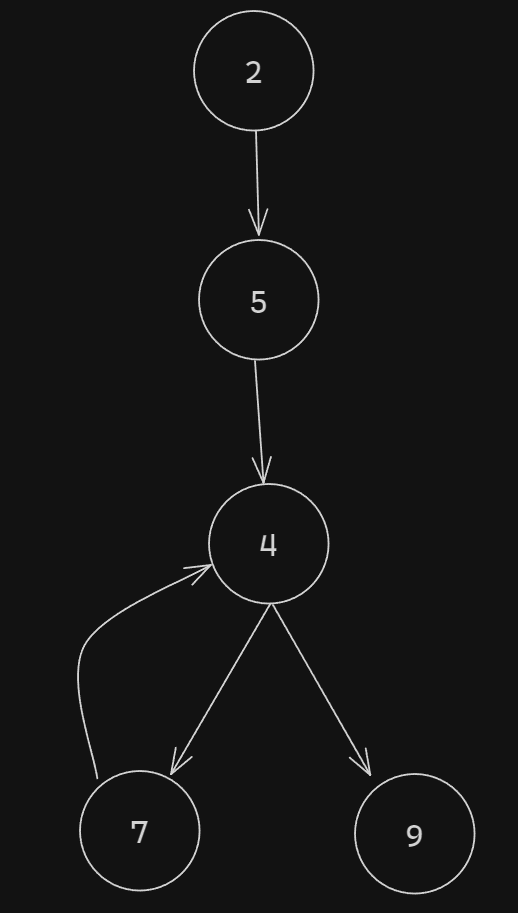
As we can see, here we have a node (7), that when (and if) we get to, it executes the statements inside of it and then goes back to one of its parents (in our case, the first-level parent).
Some other thing to note is that we have useless node, node number 5. Why is this a useless node? Well, we can just merge it with its first-level parent, node number 2.
Trying to find a general formula, off the top of my head I can define a useless node as being a node that either:
- Has its first-level parent a node that points to it and it only and the current useless node doesn't get pointed to by any other node - in which case the node can be merge with its first-level parent
- Has its first-level child a node that only it points to and it only and the child node doesn't get pointed to by any other node - in which case the node can be merged with its first-level child
Having this in mind, we can optimize:
function countToAndReturnSum(num) {
let jmp_var = 2;
while (jmp_var != 42) {
switch (jmp_var) {
case 7:
console.log(i);
sum += i;
i++;
jmp_var = 4;
break;
case 2:
var sum = 0;
var i = 1;
console.time(`countToAndReturnSum(${num})`);
jmp_var = 4;
break;
case 9:
console.timeEnd(`countToAndReturnSum(${num})`);
return sum;
break;
case 4:
jmp_var = i <= num ? 7 : 9;
break;
}
}
}
countToAndReturnSum(30);
And its corresponding diagram:
There's one more thing I want to point out before we take a look at case number 4 that contains the main reason we use this example. The thing I wanna talk about is performance (same reason I used console.time and console.timeEnd). Control Flow Flattening, besides being a great obfuscation method, it slows down the app significantly, anywhere from 15% to an even 100% time increase, depending on configuration. Have this in mind if you ever need to use it.
Now, back to our case number 4.
As you can see case 4 doesn't set our jmp_var to a specific value directly, it has the result of a ConditionalExpression.
A'ight, so how do we do this? I am a lover of simplicity, I love simple things (to not be confused with "simplistic"). So let's start with something simple, yet again: how we'd manually do it.
We start from 2, so our chain looks like: . We then move to 4 and our chain looks like: . Then we get to 7, again: . Then we get to 4 again: . And we realize that we got the case 4 2 times, so as any simple guy, I try to simplify. I realize that we are in a loop (Graph Cycle). So how would this cycle look like redone? Kowalski, Analysis:
- First, case gets executed at least once, so we could start with a do-while
- Second, are we ENTIRELY sure case executes at least once? Well, not really... So we are back to a while loop or a for loop
Is that it? For the start, yeah:
// case 4 with 7 with 4 with ...
// all instructions inside case 4 before the jmp_var assignment expression
// while with the condition
while (i <= num) {
// case 7 instructions w/o the break and jmp_var assignment expression
console.log(i);
sum += i;
i++;
// case 4 instructions w/o the break and jmp_var assignment expression
}
Let's compare it to what we had initially:
for(let i = 1; i <= num; i++){
console.log(i);
sum += i;
}
Almost identical. A few differences are that the declaration (and definition) of our counter have been extracted outside of the Loop initialization part, which is something that needs to be done by the obfuscator in order for it to be able to transform the Loop correctly. Another would be that we chose a WhileStatement instead of a ForStatement for our Loop. A simple transformation can be done and we'd get:
for(; i <= num; i++){
console.log(i);
sum += i;
}
Is everything we've done until now superficial? What happens if not just the first path takes us to a loop, but the second path, as well? Is that possible? If so, when would it be? But it can't be... It can't... The person that codes the initial script doesn't create something really complicated, they just need a loop... A for/while loop... Or maybe the obfuscator goes insane?...
KIS.
Alright enough crying and let's go for more trying. Manually going back to the original we get to:
function countToAndReturnSum(num){
var sum = 0;
var i = 1;
console.time(`countToAndReturnSum(${num})`);
for(; i <= num; i++){
console.log(i);
sum += i;
}
console.timeEnd(`countToAndReturnSum(${num})`);
return sum;
}
countToAndReturnSum(30);
Other auxiliary transformations can be put in place post-deflattening to help beautify the script even more. One of this might be tracing the Loop counter, see its references and automatically bringing its declaration and definition inside the initialization part of the Loop
function countToAndReturnSum(num){
var sum = 0;
console.time(`countToAndReturnSum(${num})`);
for(var i = 1; i <= num; i++){
console.log(i);
sum += i;
}
console.timeEnd(`countToAndReturnSum(${num})`);
return sum;
}
countToAndReturnSum(30);
3. Hard
JSCrambler says that CFF allows parametrization which increases the difficulty of reverse engineering it along with resilience against static code analysis (which is what we are doing for this specific tutorial). They mention 3 specific options: Clones (semantically equivalent clones), Dead Clones (dummy copies of basic blocks that are never executed) and Opaque Steps (which obfuscate the switching variable).
Clones are not something for today. The same can be said about Opaque Steps (we might focus on these in the future I do get some feedback from you guys that lets me know you'd want that).
Now we'll focus on the Dead Clones. These Dead Clones are paired with what we call Opaque Predicates.
There's this nice paper written by the guys over at The Pennsylvania University on Generalized Dynamic Opaque Predicates (local alternative) and another great paper written by one of the author's of the other paper, Mr. Dongpeng Xu about opaque predicates in binary code (local alternative). Both are great to continue reading after this tutorial. For now we will make use of Mr Dongpeng Xu's dissertation (2nd paper mentioned), so credits go to him.
As Mr Xu says, opaque predicates are predicates whose values are known to the obfuscator at obfuscation-time but difficult to deduce afterwards, at runtime.
In Computer Science, predicates are conditional expressions (i.e. counter <= max_len ? 1 : 2) which evaluate to either true or false.
We will exemplify the use of simple opaque predicates, getting inspiration from Mr Xu's work.
From
function countToAndReturnSum(num) {
let sum = 0;
console.time(`countToAndReturnSum(${num})`);
for (let i = 1; i <= num; i++) {
console.log(i);
sum += i;
}
console.timeEnd(`countToAndReturnSum(${num})`);
return sum;
}
countToAndReturnSum(30);
To
function countToAndReturnSum(num) {
let jmp_var = 2;
while (jmp_var != 42) {
switch (jmp_var) {
case 7:
console.log(i);
sum += i;
i++;
jmp_var = 4;
break;
case 2:
var sum = 0;
var i = 1;
console.time(`countToAndReturnSum(${num})`);
jmp_var = jmp_var * jmp_var < 0 ? 9 : 4;
break;
case 9:
console.timeEnd(`countToAndReturnSum(${num})`);
return sum;
break;
case 4:
jmp_var = i <= num ? 7 : 9;
break;
}
}
}
countToAndReturnSum(30);
The initial CFG for this:
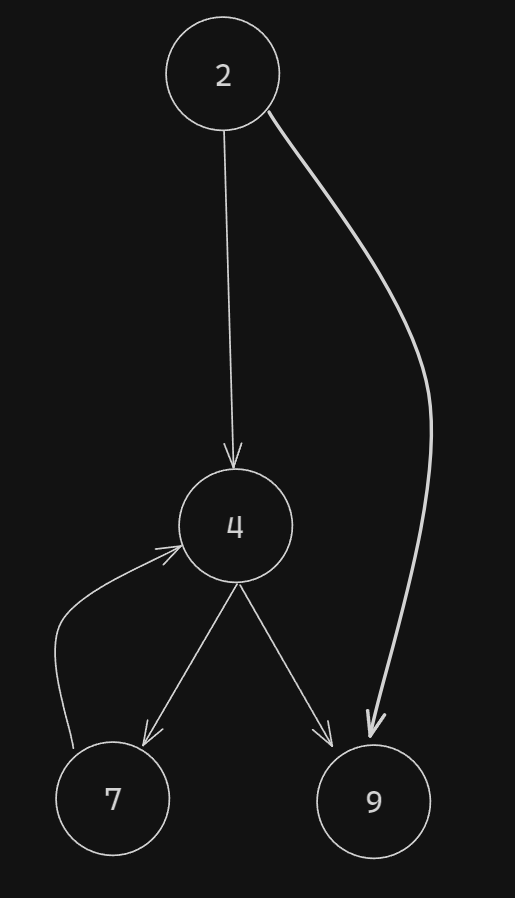
If you were not aware, we've made it so the AssignmentExpression in case number has been modified so that the right side of it doesn't point to a NumericLiteral anymore, but to a ConditionalExpression (our opaque predicate) that has the test set to (thanks to Mr Xu for the condition, Chapter 3.1 - Figure 3.1).
If our test evaluates to true, it will directly go to case (our final case that returns) and if it evaluates to false, it will continue its normal flow.
If we were to think of it logically, we conclude that so that means that our predicate would always evaluate to false. This example is one of the simple ones, in real life applications (such as DRMs, malware, etc.) they get increasingly harder to solve. They are specifically used to deter Static Analysis (which is what we are doing here) and make us opt for evaluating code.
For this to be viable we need to make sure we trace back (and in the correct order) how the variables in the condition have been modified to get to the final result.
We have to be thoughtful when doing this, as CFF is not usually alone but paired with other transformations such as checks for Code Integrity which could lead us to have different values for our variables and go down a bad path (i.e. in our case this could be that x gets to be a Complex Number which leads our predicate to be evaluated to true).
This was all just theoretical, and we won't get into it today. Let me know if I should in the future!
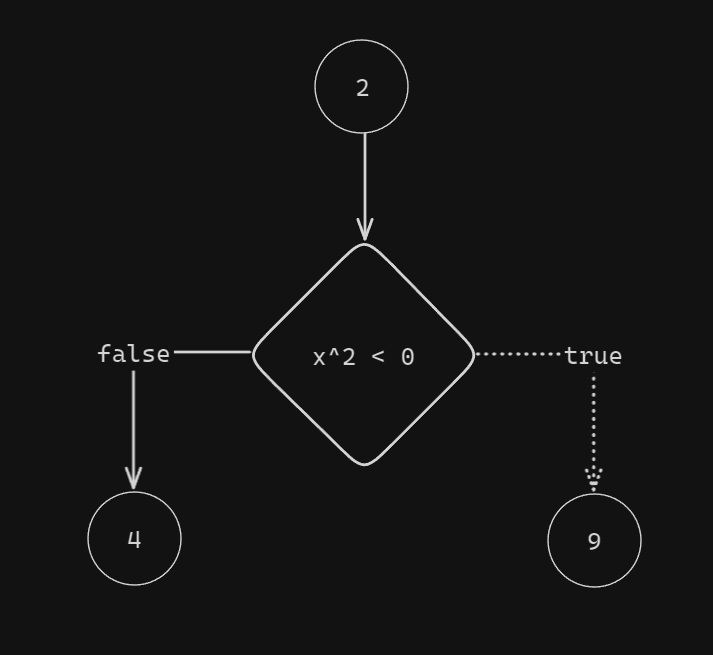
Oh, and here's Mr Xu's figure redone if you really don't wanna open his paper (you should doe, pretty good work, credits to him!).
4. Geetest
The moment you have been waiting for, playing with the Geetest script's control-flow-flattening. The current Geetest script makes use of Opaque Steps discussed previously, so, we won't touch the full file. Rather, we'll go for the first big CFF blocks of code (and inner ones) that are basic;
_gbhi.$_Ae = (function () {
var $_HIAJP = 2;
for (; $_HIAJP !== 1; ) {
switch ($_HIAJP) {
case 2:
return {
$_HIBAg: (function ($_HIBBi) {
var $_HIBCy = 2;
for (; $_HIBCy !== 14; ) {
switch ($_HIBCy) {
case 5:
$_HIBCy = $_HIBDn < $_HIBES.length ? 4 : 7;
break;
case 2:
var $_HIBFR = "", $_HIBES = decodeURI("long encrypted string");
$_HIBCy = 1;
break;
case 1:
var $_HIBDn = 0, $_HIBGf = 0;
$_HIBCy = 5;
break;
case 4:
$_HIBCy = $_HIBGf === $_HIBBi.length ? 3 : 9;
break;
case 8:
$_HIBDn++, $_HIBGf++;
$_HIBCy = 5;
break;
case 3:
$_HIBGf = 0;
$_HIBCy = 9;
break;
case 9:
$_HIBFR += String.fromCharCode(
$_HIBES.charCodeAt($_HIBDn) ^ $_HIBBi.charCodeAt($_HIBGf)
);
$_HIBCy = 8;
break;
case 7:
$_HIBFR = $_HIBFR.split("^");
return function ($_HIBHA) {
var $_HIBIe = 2;
for (; $_HIBIe !== 1; ) {
switch ($_HIBIe) {
case 2:
return $_HIBFR[$_HIBHA];
break;
}
}
};
break;
}
}
})("Ut18Py"),
};
break;
}
}
})();
For the sake of this example, we'll rename a few variables just so we have an easy time:
$_HIBIetojmp_var$_HIBCytojmp_var, as well, as it doesn't interfere in inner CFF blocks of code$_HIAJPtojmp_var, again, for the same reason: it's not referenced in inner control-flow-flattened blocks of code$_HIBBitokey, because we can easily deduce that it is related to a key for string decryption (it is passed as a StringLiteral to the IIFE)$_HIBFRtofinal_str_arr, because it is a string array resulting from the decryption$_HIBEStoenc_str, because it is the long encrypted string that we have to decrypt$_HIBDntoenc_str_index, because it is used to get the character code at its value from theenc_strvariable$_HIBGftokey_index, because it is used to get the character code at its value from thekeyvariable$_HIBHAtoindex
_gbhi.$_Ae = (function () {
var jmp_var = 2;
for (; jmp_var !== 1; ) {
switch (jmp_var) {
case 2:
return {
$_HIBAg: (function (key) {
var jmp_var = 2;
for (; jmp_var !== 14; ) {
switch (jmp_var) {
case 5:
jmp_var = enc_str_index < enc_str.length ? 4 : 7;
break;
case 2:
var final_str_arr = "",
enc_str = decodeURI("long encrypted string");
jmp_var = 1;
break;
case 1:
var enc_str_index = 0, key_index = 0;
jmp_var = 5;
break;
case 4:
jmp_var = key_index === key.length ? 3 : 9;
break;
case 8:
enc_str_index++, key_index++;
jmp_var = 5;
break;
case 3:
key_index = 0;
jmp_var = 9;
break;
case 9:
final_str_arr += String.fromCharCode(
enc_str.charCodeAt(enc_str_index) ^
key.charCodeAt(key_index)
);
jmp_var = 8;
break;
case 7:
final_str_arr = final_str_arr.split("^");
return function (index) {
var jmp_var = 2;
for (; jmp_var !== 1; ) {
switch (jmp_var) {
case 2:
return final_str_arr[index];
break;
}
}
};
break;
}
}
})("Ut18Py"),
};
break;
}
}
})();
What is the basic blueprint?
- Detect control-flow-flattened blocks
- Convert them to graphs (our custom graph implementation)
- Convert the graphs to simple chains (combining nodes accordingly) for an easy flow that a human being can track and analyze
- Replace the cff blocks with our modified blocks
One thing to mention before starting: as you can see, CFF blocks of code can be found inside one another so transformations will be done post-traversal (on node exit) because of mostly personal preference but also because we assume that the final result will be lighter in terms of nodes, thus meaning that doing them on node exit we'll speed up the process a little bit (mostly cause personal preference I am not sure how true the last statement will turn out to be).
- Set up the environment
For this specific example we will be using typescript along with the Deno runtime as I have been accustomed with running typescript with ts-node but that is too slow for me.
Thus, this is what a template ts file would look like for deno (along with types):
// @deno-types="npm:@types/babel__traverse"
import {NodePath} from "npm:@types/babel__traverse";
import {parse} from "npm:@babel/parser";
import * as t from "npm:@babel/types";
// @deno-types="npm:@types/babel__generator"
import generate_all from "npm:@babel/generator";
const generate = generate_all.default;
// @deno-types="npm:@types/babel__traverse";
import traverse_all from "npm:@babel/traverse";
const traverse = traverse_all.default;
// your code here
// ...
This will not be included in the examples just to make it a tad easier for you to go through it all.
After this is done, we also have to load the file, parse it, have a place where we can do our transformations on the AST and, in the end, to generate js from our AST and save it to a file.
// index.ts
import * as fs from "node:fs";
let AST = parse(fs.readFileSync("test.js").toString("utf-8"), {sourceType: "unambiguous"});
// Our logic here
resolveCFF(AST);
// Our logic here
fs.writeFileSync("test_out.js", generate(AST, {retainFunctionParens: true, jsonCompatibleStrings: true}).code);
- Detect control-flow-flattened blocks
For start, we will analyze just our use case, generalizing is trivial for you to do given I have spoken a little bit about how you could do it in the examples previously shown.
In our example (the geetest script) CFF blocks look something like this:
var $JMP_VAR$ = 2;
for (; $JMP_VAR$ !== 42; ) {
switch ($JMP_VAR$){
// ...
}
}
The corresponding AST looks like:
{
"type": "File",
"program": {
"type": "Program",
"sourceType": "script",
"interpreter": null,
"body": [
{
"type": "VariableDeclaration",
"declarations": [
{
"type": "VariableDeclarator",
"id": { "type": "Identifier", "name": "$JMP_VAR$" },
"init": { "type": "NumericLiteral", "value": 2 }
}
],
"kind": "var"
},
{
"type": "ForStatement",
"init": null,
"test": {
"type": "BinaryExpression",
"left": { "type": "Identifier", "name": "$JMP_VAR$" },
"operator": "!==",
"right": { "type": "NumericLiteral", "value": 42 }
},
"update": null,
"body": {
"type": "BlockStatement",
"body": [
{
"type": "SwitchStatement",
"discriminant": { "type": "Identifier", "name": "$JMP_VAR$" },
"cases": []
}
]
}
}
]
}
}
// isCFFLoop.ts
export function isCFFLoop(node: t.Node, prev: t.Node) {
return true &&
/**
* Make sure the previous statement looks roughly like this:
*
* var $JMP_VAR$ = 2;
*/
t.isVariableDeclaration(prev) &&
prev.declarations.length === 1 &&
t.isNumericLiteral(prev.declarations[0].init) &&
prev.declarations[0].init.value === 2 &&
t.isIdentifier(prev.declarations[0].id) &&
/**
* Make sure the current node is the ForStatement that we are searching for
*
* for(; $JMP_VAR$ <<OPERATOR>> NUMERIC_LITERAL;){
* // ...
* }
*/
t.isForStatement(node) &&
node.init === null &&
node.update === null &&
t.isBinaryExpression(node.test) &&
node.test.operator === "!==" &&
t.isIdentifier(node.test.left) &&
node.test.left.name === prev.declarations[0].id.name &&
/**
* Make sure the ForStatement's body is a CFF one
*
* switch($JMP_VAR$){
* // ...
* }
*/
t.isBlockStatement(node.body) &&
node.body.body.length === 1 &&
t.isSwitchStatement(node.body.body[0]) &&
t.isIdentifier(node.body.body[0].discriminant) &&
node.body.body[0].discriminant.name === prev.declarations[0].id.name
}
This leads us to:
// resolveCFF.ts
import { isCFFLoop } from "./isCFFLoop.ts";
export function resolveCFF(AST: t.Program | t.File) {
traverse(AST, {
Loop: {
exit(path: NodePath<t.Loop>) {
// get previous node
const prev_path = path.getPrevSibling();
if(prev_path.node === undefined)return;
// make sure we are at the right spot
if(!isCFFLoop(path.node, prev_path.node))return;
// now it's time to have some fun
// ...
},
},
});
}
- Convert them to graphs (our custom graph implementation)
Now it's time to convert them to graphs. For this, we'll use a custom graph implementation.
// CFFGraph.ts
export class CFFGraph {
public start: number;
public end: number;
private _vertices: Map<number, CFFNode>;
private _edges: Map<number, Set<number>>;
public jmp_var_name: string;
get edges() {
return this._edges;
}
addEdge(v1: number, v2: number) {
if (!this._edges.has(v1)) this._edges.set(v1, new Set());
// @ts-expect-error: edges.get(v1) should exist as previously set
this._edges.get(v1).add(v2);
}
get vertices() {
return this._vertices;
}
getVertex(vertex: number) {
return this._vertices.get(vertex);
}
addVertex(vertex: CFFNode) {
this._vertices.set(vertex.value, vertex);
this.addEdge(vertex.value, vertex.consequent);
if (!Number.isNaN(vertex.alternate))
this.addEdge(vertex.value, vertex.alternate);
}
constructor() {
this.start = NaN;
this.end = NaN;
this._vertices = new Map();
this._edges = new Map();
this.jmp_var_name = "";
}
prettyPrint(){
console.log("\n--\tPretty print graph\t--");
Array.from(this.vertices.values()).forEach(vertex => {
console.log(`${vertex.value} => [${vertex.consequent + (!Number.isNaN(vertex.alternate) ? ", " + vertex.alternate : "")}]`);
});
console.log("--\tPretty print graph\t--\n");
}
getParents(node_val: number){
return Array.from(this.vertices.entries()).map(([_node_val, nodes_it_points_to]) => {
if(_node_val === node_val)return undefined;
if(![nodes_it_points_to.consequent, nodes_it_points_to.alternate].includes(node_val))return undefined;
return _node_val;
}).filter(node_val => node_val !== undefined);
}
getChildren(node_val: number){
const node = this.getVertex(node_val);
if(!node)return []
const children = [node.consequent];
!Number.isNaN(node.alternate) && children.push(node.alternate);
return children;
}
}
export class CFFNode {
public value: number;
public inside: t.Statement[];
public test_expression: t.BooleanLiteral | t.BinaryExpression;
public if_true: number;
public if_false: number;
constructor(value: number, if_true?: number, if_false?: number, test_expression?: t.BooleanLiteral | t.BinaryExpression, inside?: t.Statement[]){
this.value = value;
this.test_expression = test_expression || t.booleanLiteral(true);
this.if_true = if_true || NaN;
this.if_false = if_false || NaN;
this.inside = inside || [];
}
setConsequent(consequent: number){
this.if_true = consequent;
}
setAlternate(alternate: number){
this.if_false = alternate;
}
get consequent(){
return this.if_true;
}
get alternate(){
return this.if_false;
}
}
Now, let me explain a little bit about the implementation:
CFFNode
The CFFNode class is the class that represents each SwitchCase.
The value of each CFFNode instance represents the discriminant of the SwitchCase.
The inside represents the statements that are found inside each SwitchCase, but without the final BreakStatement (that is because breaks are only needed since we are inside a SwitchStatement, but when we get rid of the CFF we won't need them anymore).
Lastly, the consequent and alternate. Let's go back a little and take a look at how the jmp_var was being updated:
$JMP_VAR$ = NUMERIC_LITERAL$JMP_VAR$ = CONDITIONAL_EXPRESSION=>$JMP_VAR$ = BINARY_EXPRESSION ? NUMERIC_LITERAL_1 : NUMERIC_LITERAL_2
The first can be written as: $JMP_VAR$ = true ? NUMERIC_LITERAL : NaN thus making us need only one type of node, the latter.
The CFFGraph class represents the whole graph. This is pretty self explanatory.
Also, we keep track of edges in the CFFGraph class while also keeping track of children nodes in each node. This works well for when we'll transform stuff.
// CFFGraph.ts
class CFFGraph {
// ...
populate(node: t.ForStatement, prev: t.Statement) {
this.jmp_var_name = (
(node.test as t.BinaryExpression).left as t.Identifier
).name;
this.start = (
(prev as t.VariableDeclaration).declarations[0].init as t.NumericLiteral
).value;
this.end = (
(node.test as t.BinaryExpression).right as t.NumericLiteral
).value;
// transform the array of switch cases to a map
// this indirectly helps us to trace just nodes that might be executed
// all other nodes (that are not connected) will be removed from the graph
const switch_statement = (node.body as t.BlockStatement)
.body[0] as t.SwitchStatement;
const switch_case_map: Map<number, t.Statement[]> = new Map();
for (const switch_case of switch_statement.cases) {
switch_case_map.set(
(switch_case.test as t.NumericLiteral).value,
switch_case.consequent.map((node) => t.cloneDeepWithoutLoc(node))
);
}
// trace from start node
const already_visited: Set<number> = new Set();
const queue: number[] = [this.start];
while (queue.length !== 0) {
const curr = queue.shift();
if (curr === undefined) break;
if (already_visited.has(curr)) continue;
already_visited.add(curr);
const curr_switch_case = switch_case_map.get(curr);
if (curr_switch_case === undefined) break;
// remove unneeded break statements
// for this example we will not get in-depth
// we'll just check the last statement to make sure it is a break and remove it
{
const last_statement = curr_switch_case.at(-1);
if (t.isBreakStatement(last_statement)) curr_switch_case.pop();
}
// find jmp_var assignment
let test_expression: t.BooleanLiteral | t.BinaryExpression =
t.booleanLiteral(true);
let if_true = NaN;
let if_false = NaN;
for (let i = 0; i < curr_switch_case.length; i++) {
const body_node = curr_switch_case.at(i);
if (!t.isExpressionStatement(body_node)) continue;
const expr = body_node.expression;
if (!t.isAssignmentExpression(expr)) continue;
if (expr.operator !== "=") continue;
if (!t.isIdentifier(expr.left)) continue;
if (expr.left.name !== this.jmp_var_name) continue;
const right = expr.right;
// remove this assignment expr
curr_switch_case.splice(i, 1);
switch (right.type) {
case "NumericLiteral":
if_true = right.value;
break;
case "ConditionalExpression":
{
if (!t.isBinaryExpression(right.test))
throw new Error(
"ConditionalExpression test is not BinaryExpression!"
);
test_expression = t.cloneDeepWithoutLoc(right.test);
if (!t.isNumericLiteral(right.consequent))
throw new Error(
"Consequent of ConditionalExpression is not a NumericLiteral, but " +
right.consequent.type
);
if (!t.isNumericLiteral(right.alternate))
throw new Error(
"Alternate of ConditionalExpression is not a NumericLiteral, but " +
right.alternate.type
);
if_true = right.consequent.value;
if_false = right.alternate.value;
}
break;
default:
throw new Error("Unknown node type: " + right.type);
}
}
// add the node to the graph
this.addVertex(
new CFFNode(
curr,
if_true,
if_false,
test_expression,
switch_case_map.get(curr)
)
);
// add children to queue to be visited
if (!Number.isNaN(if_true)) queue.push(if_true);
if (!Number.isNaN(if_false)) queue.push(if_false);
}
}
// ...
}
// resolveCFF.ts
// inside our Loop visitor
export function resolveCFF(AST: t.Program | t.File) {
traverse(AST, {
Loop: {
exit(path: NodePath<t.Loop>) {
// ...
const cff_graph = new CFFGraph();
cff_graph.populate(path.node, prev_path.node);
// for debugging purposes only
cff_graph.prettyPrint();
},
},
});
}
After running deno run index.ts we should get:
> deno run -A index.ts
-- Pretty print graph --
2 => [NaN]
-- Pretty print graph --
-- Pretty print graph --
2 => [1]
1 => [5]
5 => [4, 7]
4 => [3, 9]
7 => [NaN]
3 => [9]
9 => [8]
8 => [5]
-- Pretty print graph --
-- Pretty print graph --
2 => [NaN]
-- Pretty print graph --
- Convert the graphs to simple chains (combining nodes accordingly) for an easy flow that a human being can track and analyze
The graph that we've built last step looks like this:
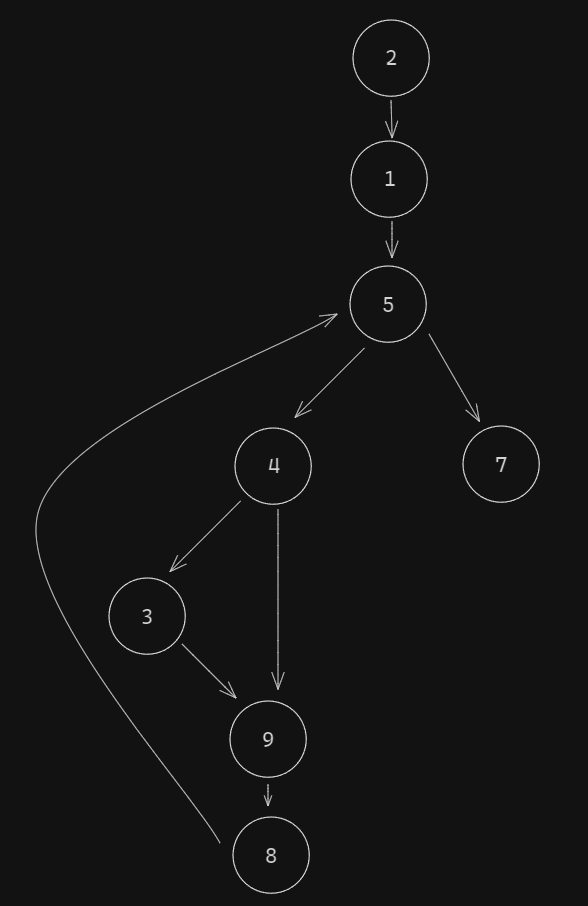
What we can observe from this is that nodes 8 and 1 are what we have previously called useless nodes (either 8 and 1 or 2 and 9, but we will consider the child node the useless node). What we can do is merge them in their parent nodes. So let's do it.
Here's the plan:
- Create method for traversing
- Create method for checking we are at a node that can be merged (only for parent nodes)
- Create method for merging
- Create method for traversing and merging useless nodes
// CFFGraph.ts
class CFFGraph {
// ...
// inspired by https://github.com/babel/babel/blob/main/packages/babel-types/src/traverse/traverseFast.ts
// 1.
static traverse({
current,
cff_graph,
enter,
exit,
state,
visited,
}: {
current: number;
cff_graph: CFFGraph;
enter?: (
node: CFFNode,
graph_ref: CFFGraph,
state: object,
visited: Set<number>
) => void;
exit?: (
node: CFFNode,
graph_ref: CFFGraph,
state: object,
visited: Set<number>
) => void;
state?: object;
visited?: Set<number>;
}) {
if (!enter && !exit) return;
const node = cff_graph.getVertex(current);
if (node === undefined) return;
if (!state) state = {};
if (!visited) visited = new Set();
if (visited.has(current)) return;
visited.add(current);
enter && enter(node, cff_graph, state, visited);
for (const child of cff_graph.getChildren(current)) {
CFFGraph.traverse({
cff_graph: cff_graph,
current: child,
enter: enter,
exit: exit,
state: state,
visited: visited,
});
}
exit && exit(node, cff_graph, state, visited);
visited.delete(current);
}
// 2.
canMergeNodeWithChildNode(node_val: number): boolean {
const children = this.getChildren(node_val);
if (children.length > 1) return false;
const childs_parents = this.getParents(children[0]);
if (childs_parents.length > 1) return false;
return true;
}
// 3.
/**
*
* @param parent_val
* @param child_val
*
* Merging is done in the parent regardless
*/
mergeNodes(parent_val: number, child_val: number) {
const parent_node = this.getVertex(parent_val);
if (!parent_node) return;
const child_node = this.getVertex(child_val);
if (!child_node) return;
if (!this.canMergeNodeWithChildNode(parent_val)) return false;
parent_node.inside.push(...child_node.inside);
parent_node.setConsequent(child_node.consequent);
parent_node.setAlternate(child_node.alternate);
parent_node.test_expression = child_node.test_expression;
this.vertices.delete(child_val);
this.edges.delete(child_val);
// @ts-expect-error: the parent exists
this.edges.get(parent_val).delete(child_val);
}
// 4.
static traverseAndMergeUselessNodes(cff_graph: CFFGraph) {
CFFGraph.traverse({
cff_graph: cff_graph,
current: cff_graph.start,
enter: (node, cff_graph) => {
if (!cff_graph.canMergeNodeWithChildNode(node.value)) return;
cff_graph.mergeNodes(node.value, cff_graph.getChildren(node.value)[0]);
return;
}
});
}
// ...
}
Finally, we can just call it in our CFF file
// resolveCFF.ts
export function resolveCFF(AST: t.Program | t.File) {
traverse(AST, {
Loop: {
exit(path: NodePath<t.Loop>) {
// ...
CFFGraph.traverseAndMergeUselessNodes(cff_graph);
cff_graph.prettyPrint();
},
},
});
}
When running index.ts this leads us to:
> deno run -A index.ts
-- Pretty print graph --
2 => [NaN]
-- Pretty print graph --
-- Pretty print graph --
2 => [5]
5 => [4, 7]
4 => [3, 9]
7 => [NaN]
3 => [9]
9 => [5]
-- Pretty print graph --
-- Pretty print graph --
2 => [NaN]
-- Pretty print graph --
As we can see, we got rid of the nodes 1 and 8! Success!
Our graph looks like this:
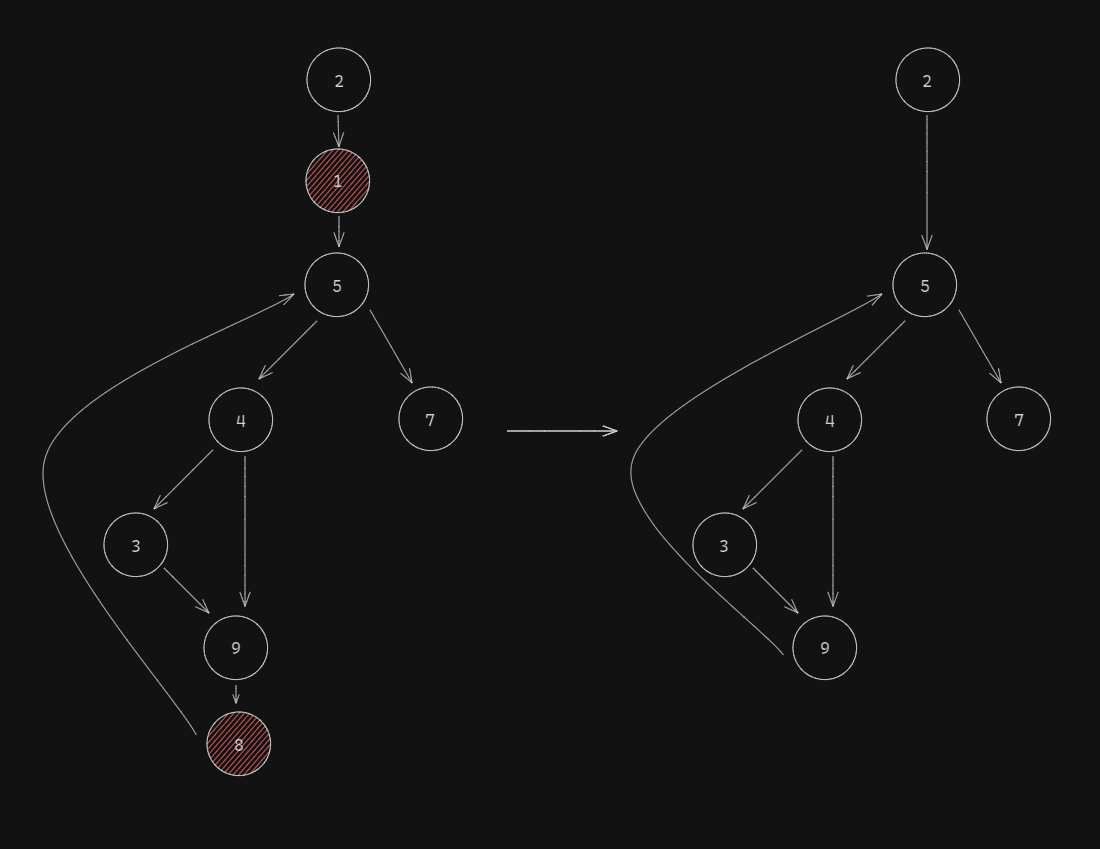
Now, let's explain a few things:
- Traverse method - the static traverse method is a custom implementation of the babel traverseFast method. But, we do have a few modifications:
- First of all, we make use of both an enter and an exit function, not just an enter function. This is great because we can make modifications both pre-child traversal and post-child traversal. The same is possible when using @babel/traverse. Might turn out useful in the future
- Second, we also keep track of the visited nodes. This is because, as opposed to traverseFast which operates on an AST in which child nodes don't directly have parent nodes as children, we do. That is because we have loops (
5 -> 4 -> 3 -> 9 -> 8 -> 5 (again)). Not keeping track of visited nodes and early returning leads us to exceed the callstack size because of too much recursion. Some of you may wonder why we use a Set: the explanation is quite simple, searching in a Set is done in O(1) (as opposed to O(n) in an Array) and since iterating through the Set's element is done in insertion order (developer.mozilla.org), an array has no net-positives in our case
- Merging - merging is done only in the parent node (in our case, while we are in node
2instead of node1and node9while we are in node8). This is for traversing fewer nodes and thus having done fewer operations to get to the same result. Merging can, in theory and practice, be done in both parent and child nodes
Next, let's take a look at node 3. As you can can see, node 3 points to node 9 and its parent, node 4, points to both 3 and 9. Here's the condition found in node 4 that decides what node we go to next: $_HIBGf === $_HIBBi.length ? 3 : 9 ($key_index === $key.length ? 3 : 9). Aha! Node 3 is basically an if statement. Okay then, so how do we figure out if a node is a Conditional Node? Starting from node 4 we fetch its children 3 and 9, we get the parents of each child node, we check to see that for one of the children the number of parents is 2 and for the other is 1, and then we check to see that one of the parents for the node that has 2 is the other node. If that's the case and everything is alright, we can merge in the parent node an IfStatement. Sounds simple, right?
// CFFGraph.ts
class CFFGraph {
// ...
static traverseAndMergeConditionalNodes(cff_graph: CFFGraph) {
CFFGraph.traverse({
cff_graph: cff_graph,
current: cff_graph.start,
enter: (node, cff_graph) => {
// 1. first we check to see that we are at the right node. in our case it will be node `4`
const children = cff_graph.getChildren(node.value);
if (children.length !== 2) return;
const [fcParents, scParents] = children.map((child) => {
return cff_graph.getParents(child);
});
if (
!(
(fcParents.length === 1 && scParents.length === 2) ||
(fcParents.length === 2 && scParents.length === 1)
)
) {
return;
}
const [childWithTwoParents, childWithOneParent, parentsOfChild] =
fcParents.length === 2
? [children[0], children[1], fcParents]
: [children[1], children[0], scParents];
if (!parentsOfChild.includes(childWithOneParent)) return;
// 2. next we attempt to merge the Conditional Node
const conditional_expr = t.cloneDeepWithoutLoc(
node.consequent === childWithOneParent
? node.test_expression
: t.unaryExpression("!", node.test_expression),
);
const to_be_appended = t.ifStatement(
conditional_expr,
t.blockStatement(
// @ts-expect-error: childWithOneParent exists as a vertex
cff_graph
.getVertex(childWithOneParent)
.inside.map((statement) => t.cloneDeepWithoutLoc(statement)),
),
);
node.inside.push(to_be_appended);
// 3. now we make sure to get rid of the Conditional Vertex
cff_graph._vertices.delete(childWithOneParent);
cff_graph._edges.delete(childWithOneParent);
// @ts-expect-error: node.value has 2 edges
cff_graph.edges.get(node.value).delete(childWithOneParent);
node.test_expression = t.booleanLiteral(true);
node.setConsequent(childWithTwoParents);
node.setAlternate(NaN);
},
});
}
// ...
}
Aaaaaaand we also add the call to this method in our resolveCFF.ts file:
// resolveCFF.ts
export function resolveCFF(AST: t.Program | t.File) {
traverse(AST, {
Loop: {
exit(path: NodePath<t.Loop>) {
// ...
CFFGraph.traverseAndMergeConditionalNodes(cff_graph);
cff_graph.prettyPrint();
},
},
});
}
And the output will look like this:
> deno run -A index.ts
-- Pretty print graph --
2 => [NaN]
-- Pretty print graph --
-- Pretty print graph --
2 => [5]
5 => [4, 7]
4 => [9]
7 => [NaN]
9 => [5]
-- Pretty print graph --
-- Pretty print graph --
2 => [NaN]
-- Pretty print graph --
The corresponding graph:
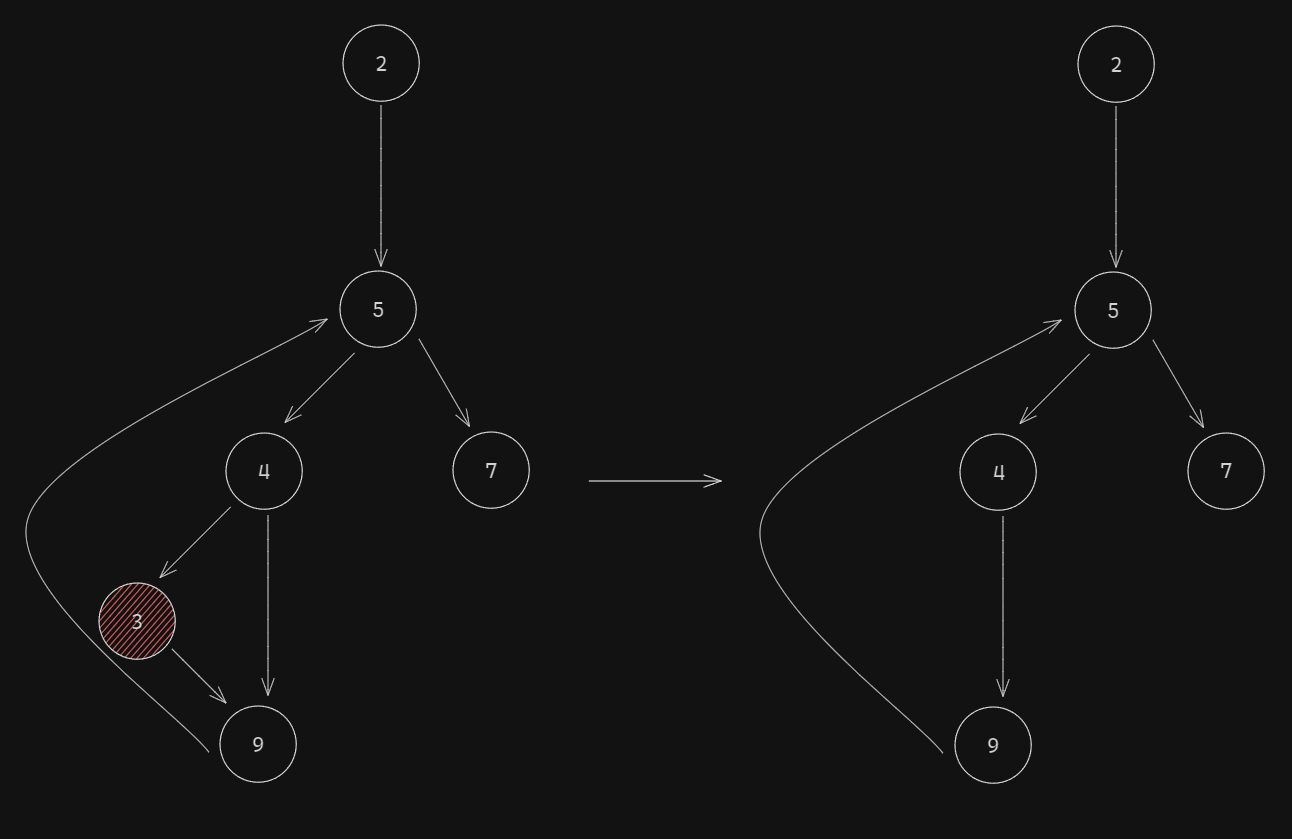
Great! But... Wait a second... Node 9 (or 4, for simplicity I'll consider 9) has now become a Useless Node. For the moment we'll call traverseAndMergeUselessNodes one more time inside our resolveCFF.ts file, and we'll touch more on this problem in the final section.
// resolveCFF.ts
export function resolveCFF(AST: t.Program | t.File) {
traverse(AST, {
Loop: {
exit(path: NodePath<t.Loop>) {
// ...
CFFGraph.traverseAndMergeUselessNodes(cff_graph);
cff_graph.prettyPrint();
},
},
});
}
This outputs:
> deno run -A index.ts
-- Pretty print graph --
2 => [NaN]
-- Pretty print graph --
-- Pretty print graph --
2 => [5]
5 => [4, 7]
4 => [5]
7 => [NaN]
-- Pretty print graph --
-- Pretty print graph --
2 => [NaN]
-- Pretty print graph --
And the corresponding graph:
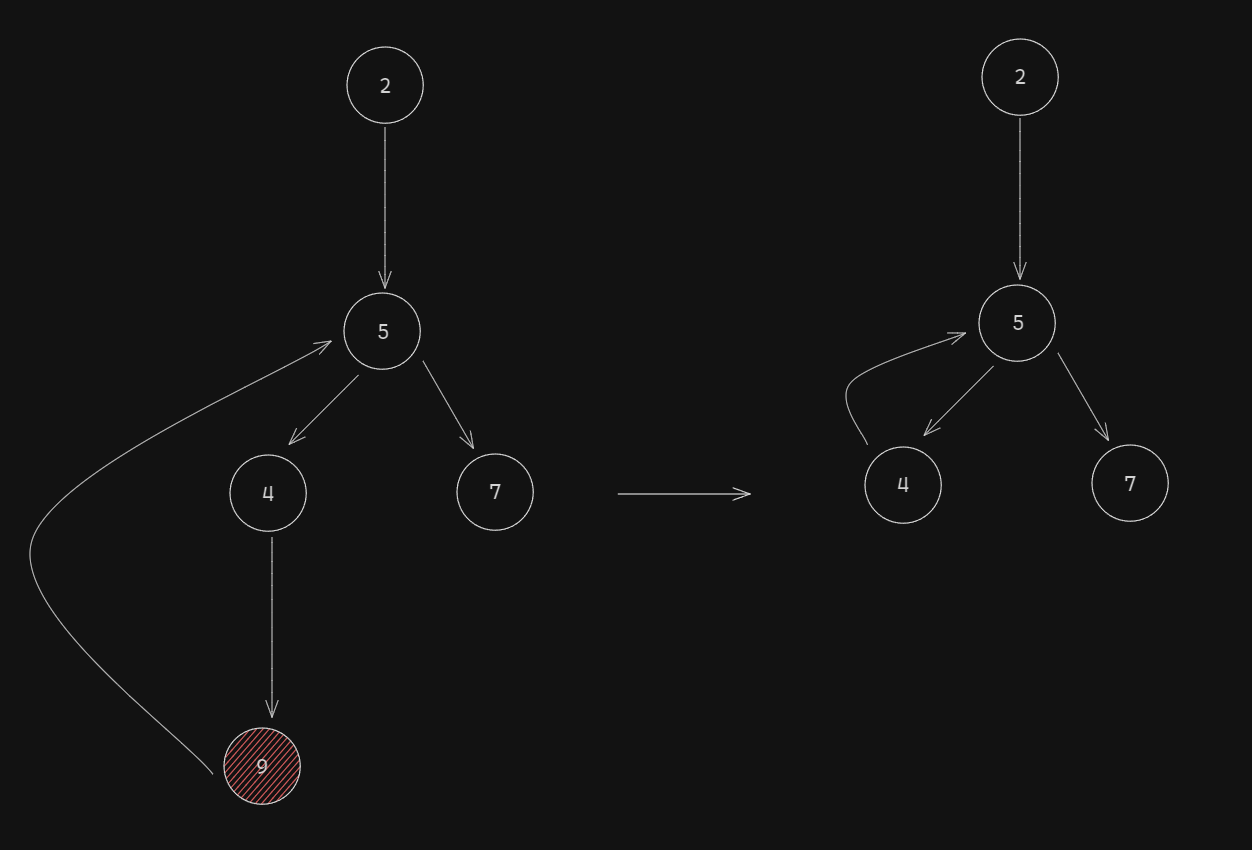
We now need to do one last transformation, and that is: to resolve the loops!
If you remember, we also keep track of the visited nodes. This means, that when we'll do this traverse, when we get to node 9 and then try to look up its children, we'll see 5, which is in the visited array. When something like this happens, we can conclude we are in a loop and merge the inside node.
// CFFGraph.ts
class CFFGraph {
// ...
// we do this transformation at the child level
// easier for me this way
static traverseAndLoopNodes(cff_graph: CFFGraph) {
CFFGraph.traverse({
cff_graph: cff_graph,
current: cff_graph.start,
enter: (node, cff_graph, _, visited) => {
// 1. we check to make sure we are at the end of a loop
const children = cff_graph.getChildren(node.value);
// we assume that any final loop node points only to the beginning of the loop
// TODO: in the future, if there's 2 children, make it so the second one is treated
// as a Conditional Node and merged
if (children.length !== 1) return;
const child = children[0];
if (!visited.has(child)) return;
const parents = cff_graph.getParents(node.value);
if (parents.length !== 1) return;
const parent = parents[0];
if (child !== parent) return;
// 2. Merge Loop Node
const parentsChildren = cff_graph.getChildren(parent);
// @ts-expect-error: parent vertex exists
const parentNode: CFFNode = cff_graph.getVertex(parent);
const loop_expr = t.cloneDeepWithoutLoc(
parentsChildren[0] === node.value
? parentNode.test_expression
: t.unaryExpression("!", parentNode.test_expression)
);
const to_be_appended = t.whileStatement(
loop_expr,
t.blockStatement(
node.inside.map((statement) => t.cloneDeepWithoutLoc(statement))
)
);
parentNode.inside.push(to_be_appended);
const isConsequent = parentsChildren[0] === node.value;
// 3. now we make sure to get rid of the Conditional Vertex
cff_graph.vertices.delete(node.value);
cff_graph.edges.delete(node.value);
// @ts-expect-error: node.value has 2 edges
cff_graph.edges.get(parent).delete(node.value);
parentNode.test_expression = t.booleanLiteral(true);
if(isConsequent){
parentNode.setConsequent(parentsChildren[1]);
parentNode.setAlternate(NaN);
}
},
});
}
// ...
}
Now we call it inside resolveCFF.ts:
// resolveCFF.ts
export function resolveCFF(AST: t.Program | t.File) {
traverse(AST, {
Loop: {
exit(path: NodePath<t.Loop>) {
// ...
CFFGraph.traverseAndLoopNodes(cff_graph);
cff_graph.prettyPrint();
},
},
});
}
This prints:
> deno run -A index.ts
-- Pretty print graph --
2 => [NaN]
-- Pretty print graph --
-- Pretty print graph --
2 => [5]
5 => [7]
7 => [NaN]
-- Pretty print graph --
-- Pretty print graph --
2 => [NaN]
-- Pretty print graph --
And the corresponding graph:
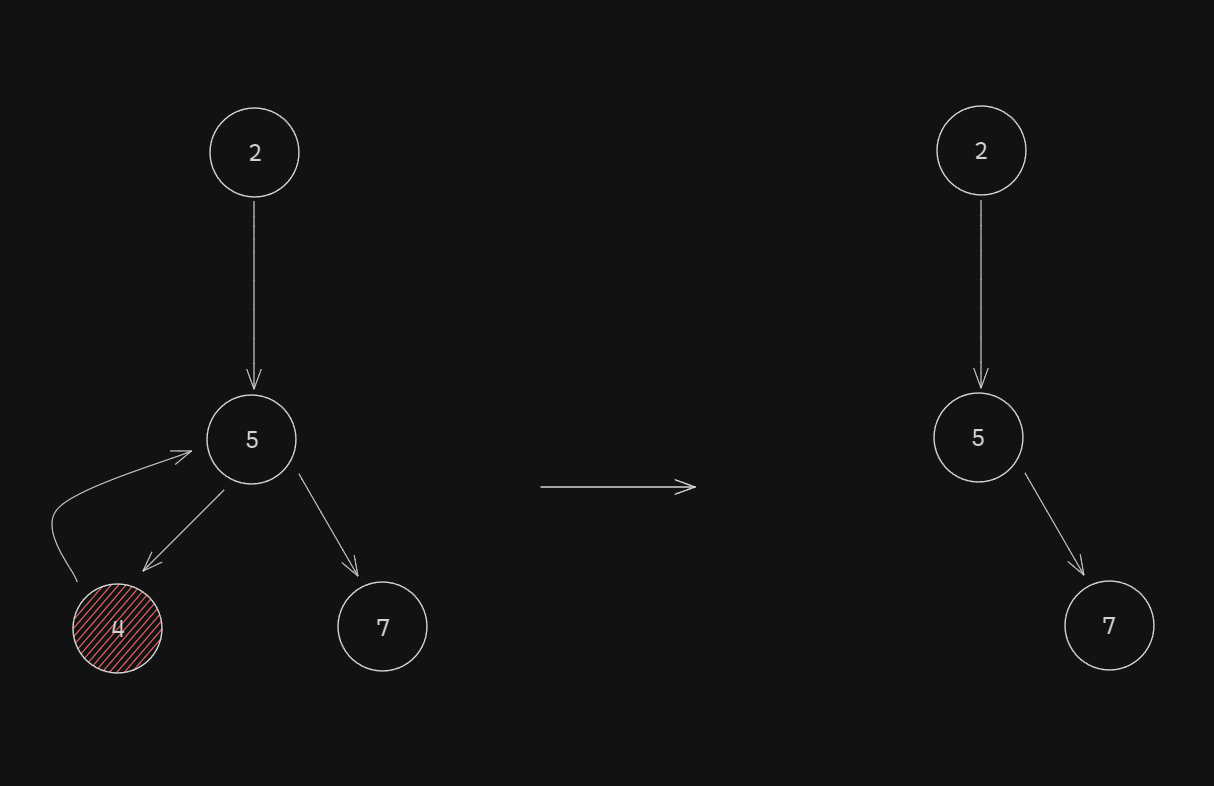
Lastly, we'll just do a simple trace function, kinda like the Useless Node merger.
// CFFGraph.ts
class CFFGraph {
// ...
static trace(cff_graph: CFFGraph): t.Statement[] {
const statements: t.Statement[] = [];
let curr = cff_graph.getVertex(cff_graph.start);
while(curr !== undefined){
statements.push(...curr.inside);
const children = cff_graph.getChildren(curr.value);
if(children.length === 2)throw new Error(`Node '${curr.value}' has 2 children`);
const child = children[0];
if(Number.isNaN(child))break;
curr = cff_graph.getVertex(child);
}
return statements;
}
// ...
}
And calling it in our resolveCFF.ts file and replacing the big for loop with the inside nodes:
// resolveCFF.ts
export function resolveCFF(AST: t.Program | t.File) {
traverse(AST, {
Loop: {
exit(path: NodePath<t.Loop>) {
// ...
prev_path.remove();
path.replaceWithMultiple(CFFGraph.trace(cff_graph));
},
},
});
}
So now, after running deno run -A index.ts, let's take a look at the final result inside our deobbed.js file:
// deobbed.js
_gbhi.$_Ae = (function () {
return {
$_HIBAg: (function ($_HIBBi) {
var $_HIBFR = "",
$_HIBES = decodeURI("LONG STRING");
var $_HIBDn = 0,
$_HIBGf = 0;
while ($_HIBDn < $_HIBES.length) {
if ($_HIBGf === $_HIBBi.length) {
$_HIBGf = 0;
}
$_HIBFR += String.fromCharCode($_HIBES.charCodeAt($_HIBDn) ^ $_HIBBi.charCodeAt($_HIBGf));
$_HIBDn++, $_HIBGf++;
}
$_HIBFR = $_HIBFR.split("^");
return function ($_HIBHA) {
return $_HIBFR[$_HIBHA];
};
})("Ut18Py")
};
})();
And now renaming variables as previously shown:
// deobbed.js
_gbhi.$_Ae = (function () {
return {
$_HIBAg: (function (key) {
var final_str_arr = "",
enc_str = decodeURI("LONG STRING");
var enc_str_index = 0,
key_index = 0;
while (enc_str_index < enc_str.length) {
if (key_index === key.length) {
key_index = 0;
}
final_str_arr += String.fromCharCode(enc_str.charCodeAt(enc_str_index) ^ key.charCodeAt(key_index));
enc_str_index++, key_index++;
}
final_str_arr = final_str_arr.split("^");
return function (index) {
return final_str_arr[index];
};
})("Ut18Py")
};
})();
Of course, this can be further beautified and we'd get something like this:
_gbhi.$_Ae = (function () {
return {
$_HIBAg: (function (key) {
let final_str_arr = "";
const enc_str = decodeURI("LONG STRING");
for(let i = 0, j = 0; i < enc_str.length; i++, j++)
while (i < enc_str.length) {
if (j === key.length) j = 0;
final_str_arr += String.fromCharCode(enc_str.charCodeAt(i) ^ key.charCodeAt(j));
}
final_str_arr = final_str_arr.split("^");
return function (index) {
return final_str_arr[index];
};
})("Ut18Py")
};
})();
Well, it's been quite a journey, but, like every other journey, it has to come to an end.
Final words
I hope you learned something and that your understanding of graphs, how to traverse them and maybe other stuff, as well, has improved. Now, there's still a few things I wanna tackle:
- By no means what I have written above is perfect. In case of a lot of nodes it might be better to also keep the parents' value inside of them and not always search the parents in the graph's edges. Fetching children might also be better to do by having a getter inside the CFFNode class that can, on the spot, transform from consequent and alternate to an array representing the children. All that I've done here is showcase my way of thinking about Control-Flow Flattened blocks through graphs. A lot can be improved.
- Now, remember when I told you that the node
4was also a Useless Node? And you also remember when I said we implement post-child traversal transformations? Well, we have to keep this in mind. First of all, it would be better if we were to modify nodes on exit, instead of modifying them on enter. Why is that? We might have loops inside of loops, or conditional nodes inside conditional nodes, or what not! If we do it on enter, only the inner-most one of these structures would get resolved (in our implementation of merging Loops this might not hold true, but from a glance I could see this being the case for Conditional Nodes - might be wrong though). While this might help a little: we are doing transformations one after the other... Manually. This is not great, this can be further improved by transforming traversals into visitors and modifying our way of traversing: we ought to, instead, traverse based on a Priority Queue. If we do this, every time we modify a node successfully (at least one operation takes place), we could place it back in the Prio Queue with the utmost priority, thus making it go through the transformations again. As it could have contained a Conditional Node inside a Loop Node inside a Useless Node, and thus we'd automatically do this without having to manually call methods.
Also, I'll leave the final files here, in case anyone wants to play with them:
If you have enjoyed this article (or not) I would really appreciate your feedback. Hmu on discord, email, or anywhere else you can find me. Oh, and... Spread the word, it really helps! Cheers and see you soon.